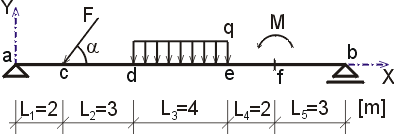
F = 20 kN, cosa = 0.6, sina = 0.8, q = 6 kN/m, M = 18 kNm.
Prostý nosník - ilustrační příklad č. 1
!!! Stránka ve výstavbě !!!

|
Určete reakce a průběhy vnitřních sil na zadaném prostém nosníku. F = 20 kN, cosa = 0.6, sina = 0.8, q = 6 kN/m, M = 18 kNm. |
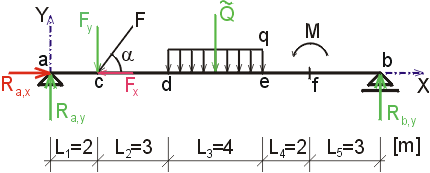 |
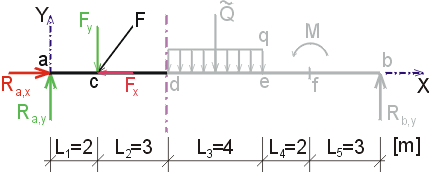
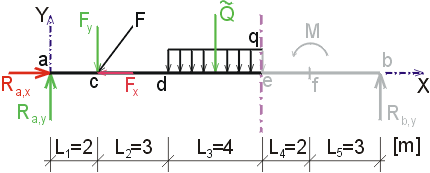
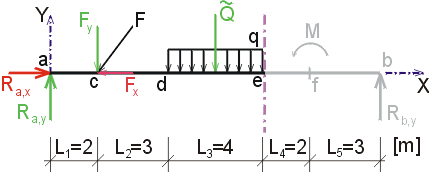
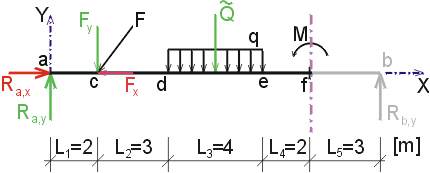
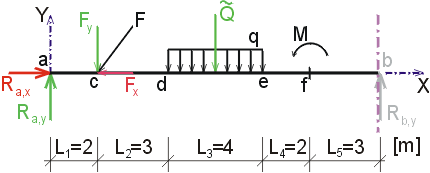
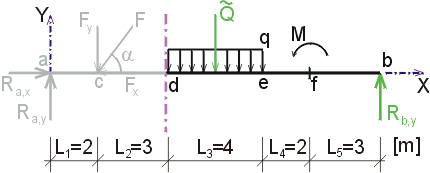
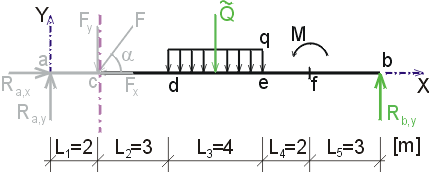
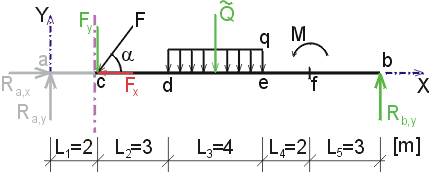
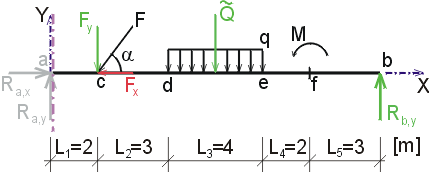
1) Výpočet reakcíNejprve rozložíme sílu F na vodorovnou složku Fx a svislou složku Fy a spojité rovnoměrné zatížení q mezi body d,e nahradíme náhradním břemenem Q, které působí v těžišti zatěžovacího obrazce :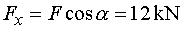 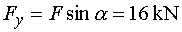 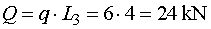 Dále nahradíme podpory složkami reakcí. Bod a je podepřen pevným neposuvným kloubem. V tomto kloubu vznikají dvě složky reakcí - vodorovná složka Ra,x a svislá složka Ra,y. Bod b je podepřen posuvným kloubem, ve kterém vzniká pouze jedna složka reakce - svislá Rb,y. Velikost neznámých složek reakcí určíme z podmínek rovnováhy : 1) 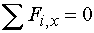 : :
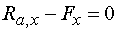 2) 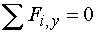 : :
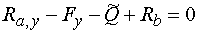 3) 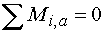 : :
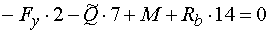 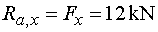 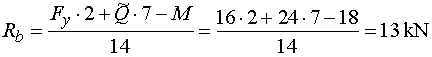 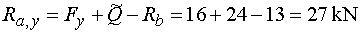 |
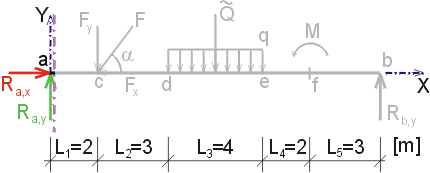 |
Na - vedeme řez v bodě a těsně zprava.
Na odříznuté části působí ve směru osy x pouze síla
Ra,x. Podle konvence kladných normálových sil působí záporně
(působí směrem do průřezu). Tedy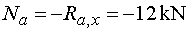 |
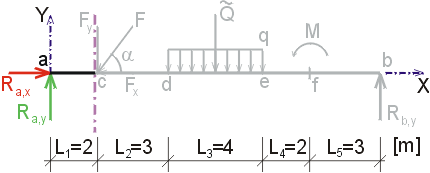 |
Ncl - vedeme řez v bodě c těsně zleva.
To znamená, že na odříznuté části nosníku nepůsobí ještě síla F.
Ve směru osy x tedy působí stále pouze síla Ra,x.
Podle konvence kladných normálových sil působí záporně (působí směrem do průřezu).
Tedy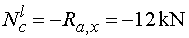 |
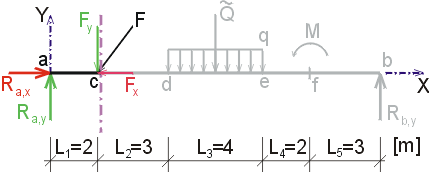 |
Ncp - vedeme řez v bodě c těsně zprava.
To znamená, že na odříznuté části nosníku již působí i síla F.
Ve směru osy x tedy působí reakce Ra,x (záporně)
a vodorovná složka Fx síly F působící
dle konvence kladně (působí ven z průřezu). Tedy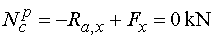 |
 |
Ndl - vedeme řez v bodě d těsně zleva.
Na odříznuté části nosníku působí ve směru osy x reakce
Ra,x (záporně) a vodorovná složka Fx (kladně).
Tedy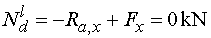 |
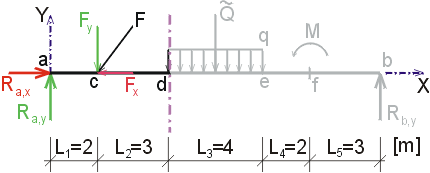 |
Ndp - vedeme řez v bodě d těsně zprava.
Na odříznuté části nosníku začíná působit spojité rovnoměrné zatížení.
To však působí ve směru osy y, takže neovlivní normálové síly.
Ve směru osy x tedy působí jen reakce Ra,x (záporně)
a vodorovná složka Fx (kladně).
Tedy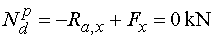 |
  |
Nel, Nep
- vedeme-li řez v bodě e těsně zleva
nebo těsně zprava (tedy na konci působení spojitého zatížení), vidíme, že
na odříznuté části nosníku nepřibylo žádné zatížení ve směru osy x,
které by vyvolalo změnu velikosti normálových sil.
Ve směru osy x tedy působí jen reakce Ra,x (záporně)
a vodorovná složka Fx (kladně).
Tedy Nel = Nep
= Ne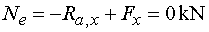 |
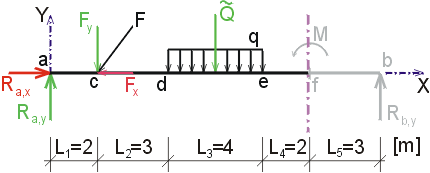  |
Nfl, Nfp
- vedeme-li řez v bodě f těsně zleva
nebo těsně zprava (tedy před místem působení osamělého momentu a za tímto místem), vidíme, že
moment neovlivní normálové síly.
Ve směru osy x tedy stále působí jen reakce Ra,x (záporně)
a vodorovná složka Fx (kladně).
Tedy Nfl = Nfp
= Nf |
 |
Nb, určujeme-li normálovou sílu v bodě b,
vedeme řez těsně zleva. Na odříznuté části stále působí ve
směru osy x jen reakce Ra,x (záporně)
a vodorovná složka Fx (kladně).
Tedy 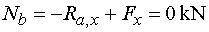 |
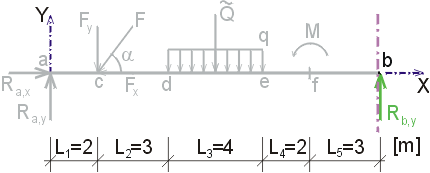 |
Nb - vedeme řez v bodě b těsně zleva.
Na odříznuté části nepůsobí ve směru osy x žádná síla.
Tedy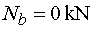 |
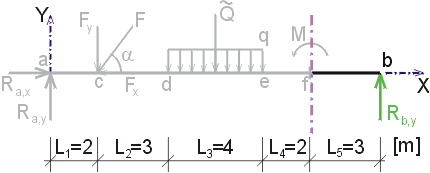 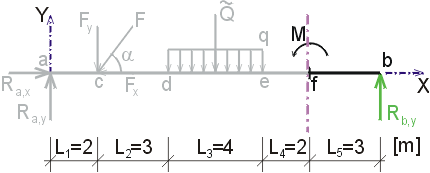 |
Nfp, Nfl
- vedeme-li řez v bodě f těsně zprava nebo těsně zleva, zjistíme, že
na odříznuté části nepůsobí ani v jednom případě ve směru osy x žádná síla. Tedy Nfp = Nfl = Nf 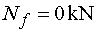 |
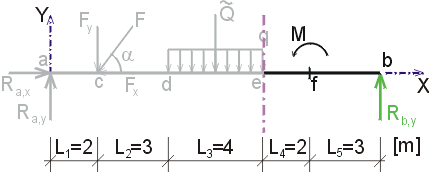 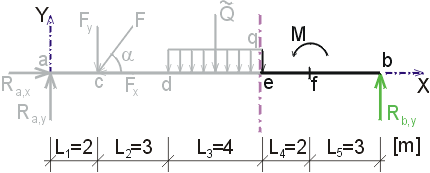 |
Nep, Nel
- vedeme-li řez v bodě e těsně zprava nebo těsně zleva, dojdeme
ke stejnému závěru jako v předchozím případě - na odříznuté části nepůsobí
ani v jednom případě ve směru osy x žádná síla. Tedy Nep = Nel = Ne 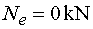 |
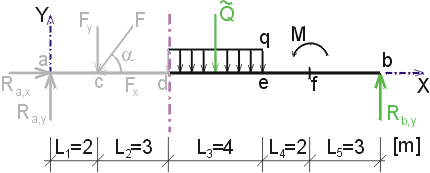  |
Ndp, Ndl
- vedeme-li řez v bodě d těsně zprava nebo těsně zleva, zjistíme, že
se opět opakuje situace z předchozích dvou případů - na odříznuté části nepůsobí
ani v jednom případě ve směru osy x žádná síla. Tedy Ndp = Ndl = Nd 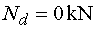 |
 |
Ncp - vedeme řez v bodě c těsně zprava,
tj. těsně před působištěm síly F. Na odříznuté části tedy stále
ještě nepůsobí žádná síla ve směru osy x.
Tedy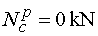 |
 |
Ncl - vedeme řez v bodě c těsně zleva,
tj. těsně za působištěm síly F. Na odříznuté části nyní již působí
zatížení ve směru osy x, a to vodorovná složka Fx.
Tato složka působí proti konvenci (působí do průřezu), tedy záporně.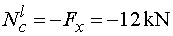 |
 |
Na - vedeme řez v bodě a těsně zprava.
Na odříznuté části působí ve směru osy x pouze vodorovná
složka Fx (záporně).
Tedy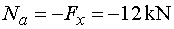 |
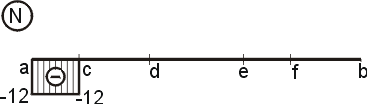
|
Máme-li vypočítány hodnoty normálových sil, můžeme nakreslit tzv. obrazec normálových sil (graf normálových sil, průběh normálových sil). Ten vykreslíme tak, že na osu nosníku vyneseme vypočítané hodnoty. Kladné hodnoty normálových sil vynášíme nad osu nosníku, záporné pod osu nosníku. Vynesené body potom spojíme odpovídajícími křivkami. V našem případě vyvolají normálové síly pouze osamělé síly Ra,x a Fx, tedy obrazec bude po částech konstantní. |
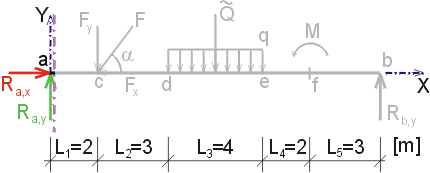 |
Va - vedeme řez v bodě a těsně zprava.
Na odříznuté části působí ve směru osy y pouze reakce
Ra,y. Podle konvence kladných posouvajících sil působí kladně.
Tedy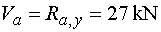 |
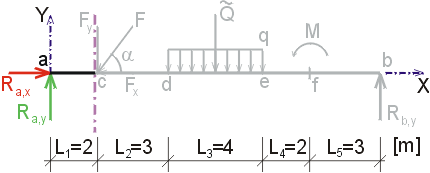 |
Vcl - vedeme řez v bodě c těsně zleva.
To znamená, že na odříznuté části nosníku nepůsobí ještě síla F.
Ve směru osy y tedy působí stále pouze reakce Ra,y
(kladně). Tedy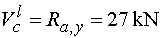 |
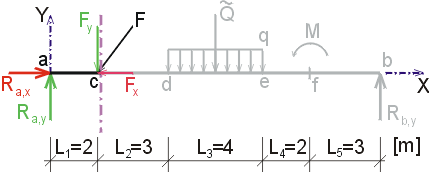 |
Vcp - vedeme řez v bodě c těsně zprava.
To znamená, že na odříznuté části nosníku již působí i síla F.
Ve směru osy y pak působí reakce Ra,y (kladně)
a svislá složka Fy síly F, která působící
proti kladné konvenci posouvajících sil, tj. záporně. Tedy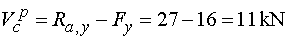 |
 |
Vdl - vedeme řez v bodě d těsně zleva.
Na odříznuté části nosníku působí ve směru osy y reakce
Ra,y (kladně) a svislá složka Fy (záporně).
Tedy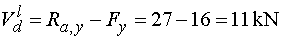 |
 |
Vdp - vedeme řez v bodě d těsně zprava.
Na odříznuté části nosníku začíná působit spojité rovnoměrné zatížení.
Účinek tohoto zatížení záleží na délce působení. Jsme-li v bodě d,
pak délka působení zatížení na odříznuté části je nulová, a proto i účinek zatížení je nulový.
Ve směru osy y tak stále působí jen reakce Ra,y (kladně)
a svislá složka Fy (záporně).
Tedy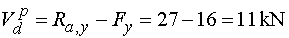 |
 |
Vel - vedeme řez v bodě e těsně zleva.
Ve směru osy y na odříznuté části nosníku působí reakce
Ra,y (kladně), svislá složka Fy (záporně)
a celé spojité rovnoměrné zatížení, jež je nahrazeno náhradním břemenem Q
(přepokládáme nulovou vzdálenosti řezu od bodu e).
Toto náhradní břemeno vyvolává taktéž zápornou posouvající sílu.
Tedy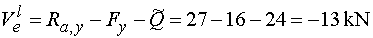 |
 |
Vep - vedeme řez v bodě e těsně zprava.
Ve směru osy y na odříznuté části nosníku působí reakce
Ra,y (kladně), svislá složka Fy (záporně)
a celé spojité rovnoměrné zatížení, jež je nahrazeno náhradním břemenem Q
působící záporně. Tedy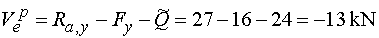 |
  |
Vfl, Vfp
- vedeme-li řez v bodě f těsně zleva
nebo těsně zprava (tedy před místem působení osamělého momentu a za tímto místem), vidíme, že
na odříznuté části nosníku nepřibyde oproti řezu v bodě e žádné další
zatížení ve směru osy y, jež by vyvolalo změnu posouvající síly.
Na levou část nosníku tak stále působí jen reakce Ra,y (kladně),
svislá složka Fy (záporně) a spojité rovnoměrné zatížení, jež
je nahrazeno náhradním břemenem Q (záporně).
Tedy Vfl = Vfp
= Vf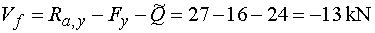 |
 |
Vb - určujeme-li posouvající sílu v bodě b,
vedeme řez těsně zleva. Na odříznuté části stále působí ve
směru osy y reakce Ra,y (kladně),
svislá složka Fy (záporně) a náhradní břemeno Q
(záporně). Tedy 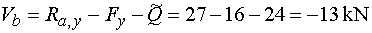 |
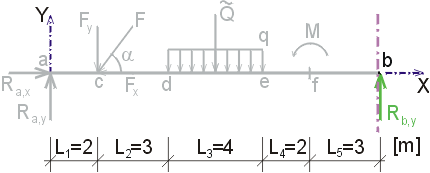 |
Vb - vedeme řez v bodě b těsně zleva.
Na odříznuté části působí ve směru osy y reakce Rb,
která podle konvence vyvolává zápornou posouvající sílu. Tedy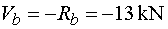 |
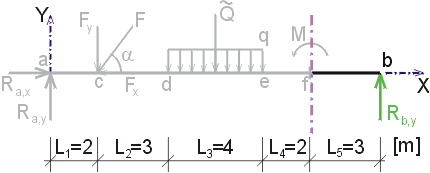 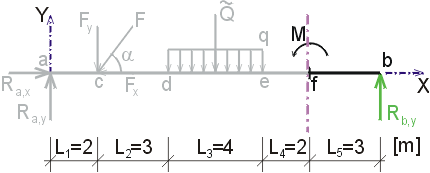 |
Vfp, Vfl
- vedeme-li řez v bodě f těsně zprava nebo těsně zleva, zjistíme, že
na odříznuté části působí ve směru osy y v obou případech pouze
reakce Rb (záporně).
Tedy Vfp = Vfl
= Vf 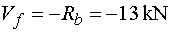 |
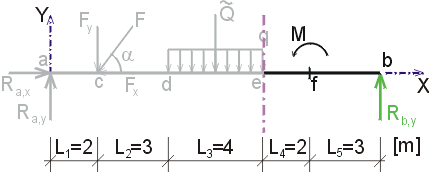 |
Vep - vedeme řez v bodě e těsně zprava.
Na odříznuté části působí ve směru osy y pouze
reakce Rb (záporně). Tedy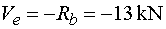 |
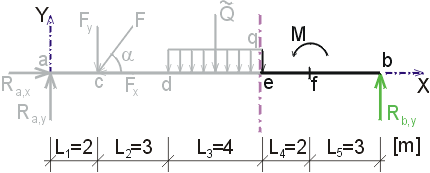 |
Vel - vedeme řez v bodě e těsně zleva.
Na odříznuté části působí ve směru osy y reakce Rb (záporně)
a dále začíná působit spojité zatížení. Délka působení tohoto zatížení na
odříznuté části je však nulová a tedy i účinek zatížení je nulový. Tedy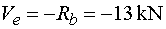 |
 |
Vdp - vedeme řez v bodě d těsně zprava.
Na odříznuté části působí ve směru osy y reakce Rb (záporně)
a celé spojité rovnoměrné zatížení (za předpokladu nulové vzdálenosti bodu d
od místa řezu), jež je nahrazeno náhradním břemenem Q,
které vyvolá kladnou posouvající sílu.
Tedy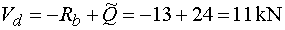 |
 |
Vdl - vedeme řez v bodě d těsně zleva.
Na odříznuté části působí ve směru osy y reakce Rb (záporně)
a celé spojité rovnoměrné zatížení, jež je nahrazeno náhradním břemenem Q,
které vyvolá kladnou posouvající sílu. Tedy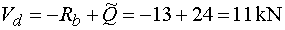 |
 |
Vcp - vedeme řez v bodě c těsně zprava,
tj. těsně před působištěm síly F.
Na odříznuté části působí ve směru osy y reakce Rb (záporně)
a náhradní břemeno Q (kladně). Tedy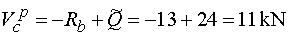 |
 |
Vcl - vedeme řez v bodě c těsně zleva,
tj. těsně za působištěm síly F. Na odříznuté části nyní působí
ve směru osy y kromě reakce Rb (záporně)
a náhradního břemena Q (kladně) také svislá složka Fy,
působicí taktéž kladně. Tedy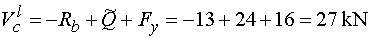 |
 |
Va - vedeme řez v bodě a těsně zprava.
Na odříznuté části působí ve směru osy y reakce Rb (záporně),
náhradní břemeno Q (kladně) a svislá složka Fy (kladně).
Tedy |
|
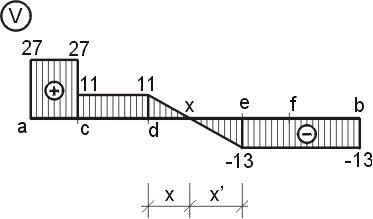
Máme-li vypočítány hodnoty posouvajících sil, můžeme nakreslit tzv. obrazec posouvajících sil
(graf posouvajících sil, průběh posouvajících sil).
Ten vykreslíme tak, že na osu nosníku vyneseme vypočítané hodnoty. Kladné hodnoty
posouvajících sil vynášíme nad osu nosníku, záporné pod osu nosníku. Vynesené body potom
spojíme odpovídajícími křivkami. Mezi body a,c a c,d bude
průběh konstantní, mezi body d,e bude průběh lineární, protože
mezi body působí rovnoměrné spojité zatížení, a mezi body e,f,b
bude průběh opět konstantní. Z obrazce vidíme, že mezi body e,d protíná graf osu nosníků (osu x). Takovému místu říkáme "nebezpečný" průřez, poněvadž v tomto místě vzniká mezi body d,e maximální ohybový moment. Musíme tedy přesně stanovit toto místo x. |
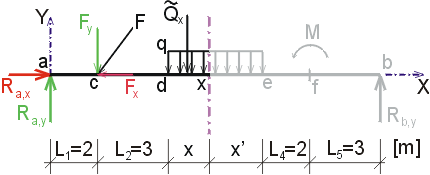
|
Určení hodnoty x zleva Vedeme-li řez mezi body d,e v místě x, tak posouvající sílu vyvodí reakce Ra,y, složka Fy a část spojitého zatížení q působicího na délce x. Náhradní břemeno Qx má velikost Qx=q.x. Potom pro velikost posouvající síly platí : 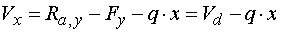 My hledáme takové x, pro které platí 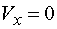 tedy hledáme řešení rovnice 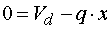 Řešením tohoto vztahu dostáváme vztah pro hledanou hodnotu x : 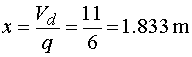 |
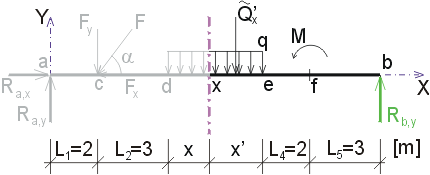
|
Určení hodnoty x' zprava Vedeme-li řez mezi body d,e v místě x, tak posouvající sílu vyvodí reakce Rb a část spojitého zatížení q působicího na délce x'. Náhradní břemeno Q'x má velikost Q'x =q.x'. Potom pro velikost posouvající síly platí : 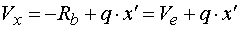 My hledáme takové x', pro které platí 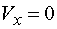 tedy hledáme řešení rovnice 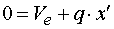 Řešením tohoto vztahu dostáváme vztah pro hledanou hodnotu x' : 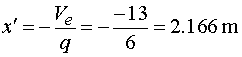 |
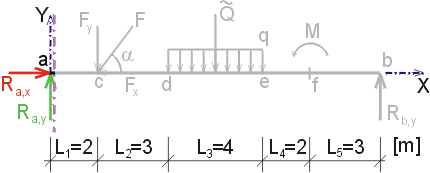 |
Ma - vedeme řez v bodě a těsně zprava.
Na odříznuté části působí reakce Ra,x a Ra,y.
Složka Ra,x nevyvodí moment k bodu řezu, protože paprsek reakce
prochází řezem. Složka Ra,y prochází
bodem a, takže také nevyvodí moment k řezu (přepokládáme, že
vzdálenost bodu a od řezu je nulová).
Tedy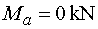 |
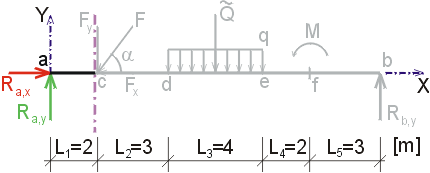 |
Mcl - vedeme řez v bodě c těsně zleva.
To znamená, že na odříznuté části nosníku nepůsobí ještě síla F.
Na odříznuté části působí reakce Ra,x a Ra,y.
Složka Ra,x nevyvodí moment k bodu řezu, protože paprsek reakce
opět prochází řezem (paprsek prochází všemi body nosníku, takže v žádném řezu nevyvodí moment).
Složka Ra,y působí na rameni L1
a vyvodí moment, který bude otáčet kolem bodu c podle konvence kladně
(tedy bude táhnout dolní vlákna). Tedy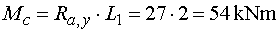 |
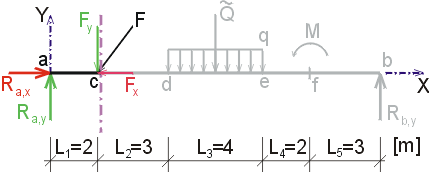 |
Mcp - vedeme řez v bodě c těsně zprava.
To znamená, že na odříznuté části nosníku již působí i síla F.
Z odříznuté části vyvodí moment pouze reakce Ra,y
na rameni L1 otáčející kladně.
Složka Fx stejně jako reakce Ra,x
nevyvodí moment, protože prochází bodem řezu. Složka Fy působí
v bodě c a za předpokladu, že vzdálenost místa řezu od bodu c
je nulová, nevyvodí ani složka Fy moment k bodu c.
Tedy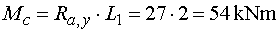 |
 |
Mdl - vedeme řez v bodě d těsně zleva.
Z odříznuté části nosníku vyvodí moment reakce Ra,y
a složka Fy. Reakce Ra,y
působí na rameni (L1+L2) a kolem bodu
d otačí kladně (táhne dolní vlákna).
Složka Fy působí na rameni L2
a kolem bodu d otačí proti kladné konvenci, tj. záporně (tlačí dolní vlákna)
Výsledný ohybový moment v řezu je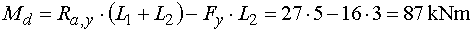 |
 |
Mdp - vedeme řez v bodě d těsně zprava.
Na odříznuté části nosníku začíná působit spojité rovnoměrné zatížení.
Účinek totoho zatížení záleží na délce působení. Jsme-li v bodě d,
pak délka působení zatížení na odříznuté části je nulová, a proto i účinek zatížení
je nulový (nevyvodí moment obdobně jako nevyvodí posouvající sílu).
Z odříznuté části nosníku vyvodí moment opět reakce Ra,y
a složka Fy jako v předchozím řezu. Obě síly působí
také na shodných ramenech a otáčí stejným směrem, takže platí stejný vztah :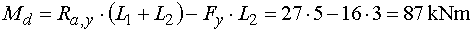 |
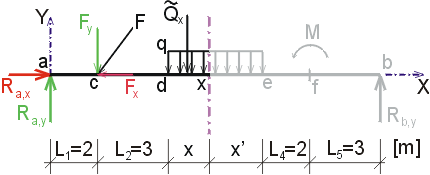 |
Mx - protože jsme při výpočtu posouvajicích sil
nalezli nebezpečný průřez, musíme v tomto řezu určit velikost momentu.
Vedeme tedy řez v bodě x.
Z odříznuté části nosníku vyvodí moment reakce Ra,y,
složka Fy a náhradní břemeno Qx,
jež nahrazuje část spojitého zatížení působicího na odříznuté části.
Reakce Ra,y působí na rameni (L1+
L2+x) a otáčí kladně.
Složka Fy působí na rameni (L2+
x) a otáčí záporně. Náhradní břemeno Qx působí na rameni
x/2 a otáčí také záporně. Výsledný ohybový moment v řezu je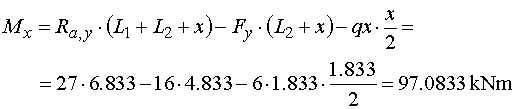 |
 |
Mel - vedeme řez v bodě e těsně zleva.
Z odříznuté části nosníku vyvodí moment reakce Ra,y,
složka Fy a náhradní břemeno Q
(předpokládáme, že vzdálenost řezu k bodu e je nulová).
Reakce Ra,y působí na rameni (L1+
L2+L3) a kolem bodu
e otačí podle konvence kladně (táhne dolní vlákna).
Složka Fy působí na rameni (L2+
L3) a kolem bodu e otáčí podle konvence
záporně (tlačí do dolních vláken). Náhradní břemeno Q působí na rameni
L3 /2 a kolem bodu e otáčí podle konvence záporně
(tlačí dolní vlákna). Výsledný ohybový moment v řezu je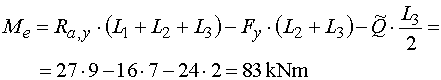 |
 |
Mep - vedeme řez v bodě e těsně zprava.
Z odříznuté části nosníku vyvodí moment opět reakce Ra,y,
složka Fy a náhradní břemeno Q.
Všechny síly působí na stejných ramenech a otáčejí stejným směrem jako v přechozím
řezu. Takže platí stejný vztah :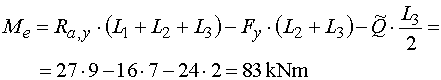 |
 |
Mfl - vedeme řez v bodě f těsně zleva
(tedy před místem působení osamělého momentu).
Z odříznuté části nosníku vyvodí moment opět reakce Ra,y,
složka Fy a náhradní břemeno Q.
Všechny síly otáčejí kolem bodu f stejným směrem jako v předchozích
dvou řezech (mají tedy stejná znamánka). Působí však na jiných ramenech.
Reakce Ra,y na rameni
(L1+L2+L3+L4)=
(L-L5), složka Fy
na rameni (L2+L3+L4)
a náhradní břemeno Q na rameni (L3 /2+L4).
Výsledný moment je :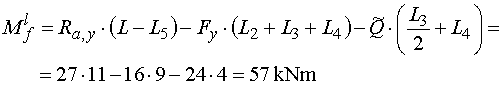 |
 |
Mfp - vedeme řez v bodě f těsně zprava
(tedy za místem působení osamělého momentu).
Z odříznuté části nosníku vyvodí moment reakce Ra,y,
složka Fy, náhradní břemeno Q a osamělý
moment M.
Všechny síly působí na stejných ramenech a otáčejí kolem bodu f
stejným směrem jako v předchozím řezu. Navíc zde působí moment M,
který otačí podle konvence záporně.
Výsledný moment je :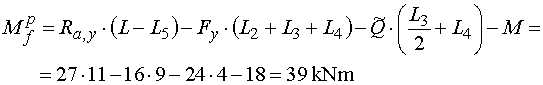 |
 |
Mb - určujeme-li ohybový moment v bodě b,
vedeme řez těsně zleva.
Z odříznuté části vyvodí moment reakce Ra,y na rameni
L (otáčí kladně), složka Fy na rameni
(L-L1) (záporně), náhradní břemeno Q
na rameni (L3 /2+L4+L5)
(záporně) a moment M (záporně).
Výsledný moment je :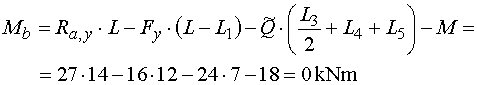 |
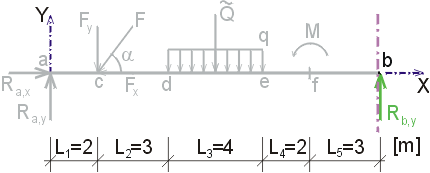 |
Mb - vedeme řez v bodě b těsně zleva.
Na odříznuté části působí pouze reakce Rb, která
nevyvodí k místu řezu moment, poněvadž předpokládáme, že vzdálenost řezu
od bodu b je nulová.
Tedy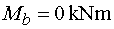 |
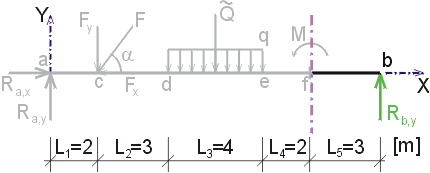 |
Mfp - vedeme řez v bodě f
těsně zprava (tedy před místem působení osamělého momentu).
Z odříznuté části moment vyvodí pouze reakce Rb
působící na rameni L5 a otáčející podle konvence kladně.
Tedy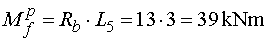 |
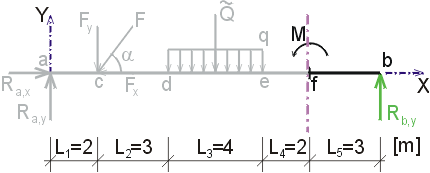 |
Mfp - vedeme řez v bodě f
těsně zleva (tedy za místem působení osamělého momentu).
Z odříznuté části moment vyvodí reakce Rb a osamělý
moment M. Reakce Rb
působí na rameni L5 a otáčejí kolem bodu f
podle konvence kladně. Osamělý moment M otáčí také kladně.
Tedy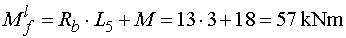 |
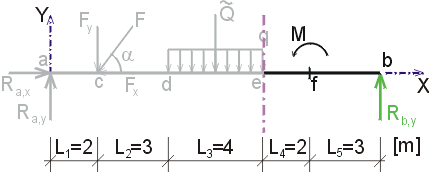 |
Mep - vedeme řez v bodě e těsně zprava.
Z odříznuté části vyvodí moment reakce Rb a
osamělý moment M. Reakce Rb působí
na rameni (L4 + L5)
a otáčí kladně. Moment taktéž otáčí kladně. Tedy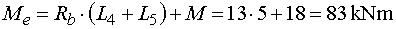 |
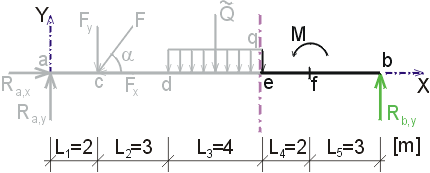 |
Mel - vedeme řez v bodě e těsně zleva.
Na odříznuté části nosníku začíná působit spojité rovnoměrné zatížení.
Účinek totoho zatížení záleží na délce působení. Jsme-li v bodě e,
pak délka působení zatížení na odříznuté části je nulová, a proto i účinek zatížení
je nulový (nevyvodí moment obdobně jako nevyvodí posouvající sílu).
Z odříznuté části nosníku vyvodí moment reakce Rb
a osamělý moment M na shodných ramenech jako v předchozím řezu.
Platí proto stejný vztah :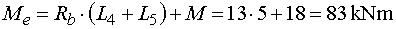 |
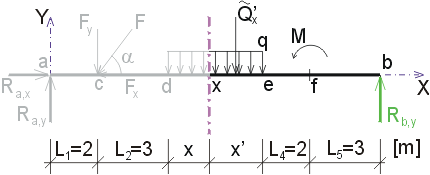 |
Mx - protože jsme při výpočtu posouvajicích sil
nalezli nebezpečný průřez, musíme v tomto řezu určit velikost momentu.
Vedeme tedy řez v bodě x.
Z odříznuté části nosníku vyvodí moment reakce Rb,
osamělý moment M a náhradní břemeno Q'x,
jež nahrazuje část spojitého zatížení působicího na odříznuté části.
Reakce Rb působí na rameni (x'+
L4+L5) a otáčí kladně.
Osamělý moment otáčí také kladně a náhradní břemeno Q'x
působí na rameni x'/2 a otáčí záporně.
Výsledný ohybový moment v řezu je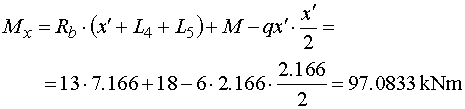 |
 |
Mdp - vedeme řez v bodě d těsně zprava.
Z odříznuté části vyvodí moment k místu řezu reakce Rb,
osamělý moment M a náhradní břemeno Q
(předpokládáme, že vzdálenost řezu k bodu e je nulová).
Reakce Rb působí na rameni (L3+
L4+L5) a otáčí kladně.
Osamělý moment M také otáčí kladně a náhradní břemeno
Q působí na rameni (L3 /2) a otáčí
proti konvenci, tedy záporně. Pro výsledný ohybový moment platí :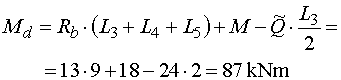 |
 |
Mdp - vedeme řez v bodě d těsně zleva.
Z odříznuté části vyvodí moment k místu řezu reakce Rb,
osamělý moment M a náhradní břemeno Q.
Obě síly a moment působí na stejných ramenech a otáčejí stejným směrem
jako v přechozím řezu. Takže platí stejný vztah :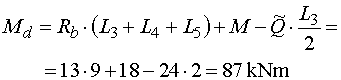 |
 |
Mcp - vedeme řez v bodě c těsně zprava.
To znamená, že na odříznuté části nosníku nepůsobí ještě síla F.
Z odříznuté části vyvodí moment k místu řezu reakce Rb,
osamělý moment M a náhradní břemeno Q.
Reakce Rb působí na rameni (L-
L1) a otáčí kladně. Osamělý moment M
také otáčí kladně a náhradní břemeno Q působí na rameni
(L2+L3 /2) a otáčí záporně.
Pro výsledný ohybový moment platí vztah: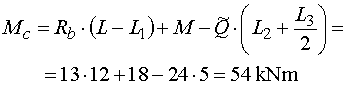 |
 |
Mcl - vedeme řez v bodě c těsně zleva.
To znamená, že na odříznuté části nosníku již působí i síla F.
Její složky Fx a Fy ale
nevyvodí k místu řezu moment, poněvadž složka Fx
prochází bodem c a složka Fy působí
na nulovém rameni. Moment k místu řezu tedy vyvodí pouze reakce Rb,
osamělý moment M a náhradní břemeno Q. Obě
síly i moment působí na stejných ramenech a otáčejí stejným směrem jako
v předchozím případě, proto platí stejný vztah :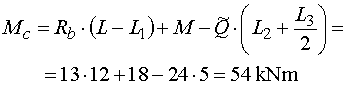 |
 |
Ma - vedeme řez v bodě a těsně zprava.
Z odříznuté části vyvodí moment reakce Rb, osamělý moment
M, náhradní břemeno Q a složka Fy.
Reakce Rb působí na rameni L a otáčí kladně,
osamělý moment M otáčí také kladně, náhradní břemeno Q
působí na rameni (L1+L2+L3 /2)
a otáčí záporně a složka Fy působí na rameni L1
a otáčí také záporně. Pro výsledný moment platí tedy vztah :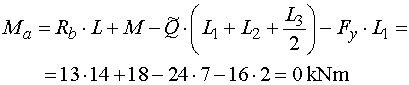 |
|
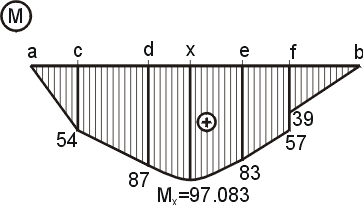
Máme-li vypočítány hodnoty ohybových momentů, můžeme vykreslit tzv. obrazec ohybových momentů (graf ohybových momentů, průběh ohybových momentů). Ten vykreslíme tak, že na osu nosníku vyneseme vypočítané hodnoty. POZOR ! Kladné hodnoty ohybových momentu vynášíme pod osu nosníku, záporné nad osu nosníku. Vynesené body potom spojíme odpovídajícími křivkami. Mezi body a,c a c,d bude průběh lineární, mezi body d,e bude průběh parabolický, protože mezi body působí rovnoměrné spojité zatížení, a mezi body e,f,b bude průběh opět lineární. |